sphtriangulate
sphtriangulate(cmd0::String="", arg1=nothing, kwargs...)keywords: GMT, Julia, Delaunay spherical triangulation, Voronoi
Delaunay or Voronoi construction of spherical data.
Description
Reads lon, lat from file or table and performs a spherical Delaunay triangulation, i.e., it determines how the points should be connected to give the most equilateral triangulation possible on the sphere. Optionally, you may choose voronoi=:v which will do further processing to obtain the Voronoi polygons. Normally, either set of polygons will be written as closed fillable segment output; use arcs=true to write unique arcs instead. As an option, compute the area of each triangle or polygon. The algorithm used is STRIPACK.
Required Arguments
table
One or more data tables holding a number of data columns.
Optional Arguments
A or area : – area=true
Compute the area of the spherical triangles (voronoi=:d) or polygons (voronoi=:v) and write the areas (in chosen units; see unit) in the output segment headers [no areas calculated].
C or save_mem : – save_mem=true
For large data set you can save some memory (at the expense of more processing) by only storing one form of location coordinates (geographic or Cartesian 3-D vectors) at any given time, translating from one form to the other when necessary [Default keeps both arrays in memory].
D or skipdup : skipdup=true
Used to skip the last (repeated) input vertex at the end of a closed segment if it equals the first point in the segment. [Default uses all points].
L or unit : – unit=??
Specify the unit used for distance and area calculations. Choose among unit=:e (m), f (foot), k (km), M (mile), n (nautical mile), u (survey foot), or d (spherical degree). A spherical approximation is used unless spherical_dist=:ellipsoidal is set, in which case we convert latitudes to authalic latitudes before calculating areas. When degree is selected the areas are given in steradians.
N or nodes : – nodes="file"
Write the information pertaining to each polygon. For Delaunay: the three node number and the triangle area (if area was set); for Voronoi the unique node lon, lat and polygon area (if area was set)) to a separate file. This information is also encoded in the segment headers of ASCII output files (or dataset types). Required if binary output is needed.
Q or voronoi : – voronoi=:d|v
Use voronoi=:d for Delaunay triangles or voronoi=:v for Voronoi polygons [Delaunay]. If binary_out is used then nodes may be used to specify a separate file where the polygon information normally is written.
T or arcs : – arcs=true
Write the unique arcs of the construction [Default writes fillable triangles or polygons]. When used with area we store arc length in the segment header in chosen unit (see unit).
V or verbose : – verbose=true | verbose=level
Select verbosity level. More at verbose
bi or binary_in : – binary_in=??
Select native binary format for primary table input. More at
di or nodata_in : – nodata_in=??
Substitute specific values with NaN. More at
e or pattern : – pattern=??
Only accept ASCII data records that contain the specified pattern. More at
g or gap : – gap=??
Examine the spacing between consecutive data points in order to impose breaks in the line. More at
h or header : – header=??
Specify that input and/or output file(s) have n header records. More at
j or metric or spherical_dist or spherical : – metric=greatcirc or spherical=:flat or spherical=:ellipsoidal
Determine how spherical distances are calculated in modules that support this [Default isspherical=:greatcirc]. GMT has different ways to compute distances on planetary bodies:
- spherical=:greatcirc to perform great circle distance calculations, with parameters such as distance
increments or radii compared against calculated great circle distances [Default is spherical=:greatcirc].
- spherical=:flat to select Flat Earth mode, which gives a more approximate but faster result.
- spherical=:ellipsoidal to select ellipsoidal (or geodesic) mode for the highest precision
and slowest calculation time.
Note: All spherical distance calculations depend on the current ellipsoid (PROJ_ELLIPSOID),
the definition of the mean radius (PROJ_MEAN_RADIUS), and the specification of latitude type
(PROJ_AUX_LATITUDE). Geodesic distance calculations is also controlled by method (PROJ_GEODESIC).
q or inrows : – inrows=??
Select specific data rows to be read and/or written. More at
s or skiprows or skip_NaN : – skip_NaN=true | skip_NaN="<cols[+a][+r]>"
Suppress output of data records whose z-value(s) equal NaN. More at
yx : – yx=true
Swap 1st and 2nd column on input and/or output. More at
r or reg or registration : – reg=:p | reg=:g
Select gridline or pixel node registration. Used only when output is a grid. More at
Examples
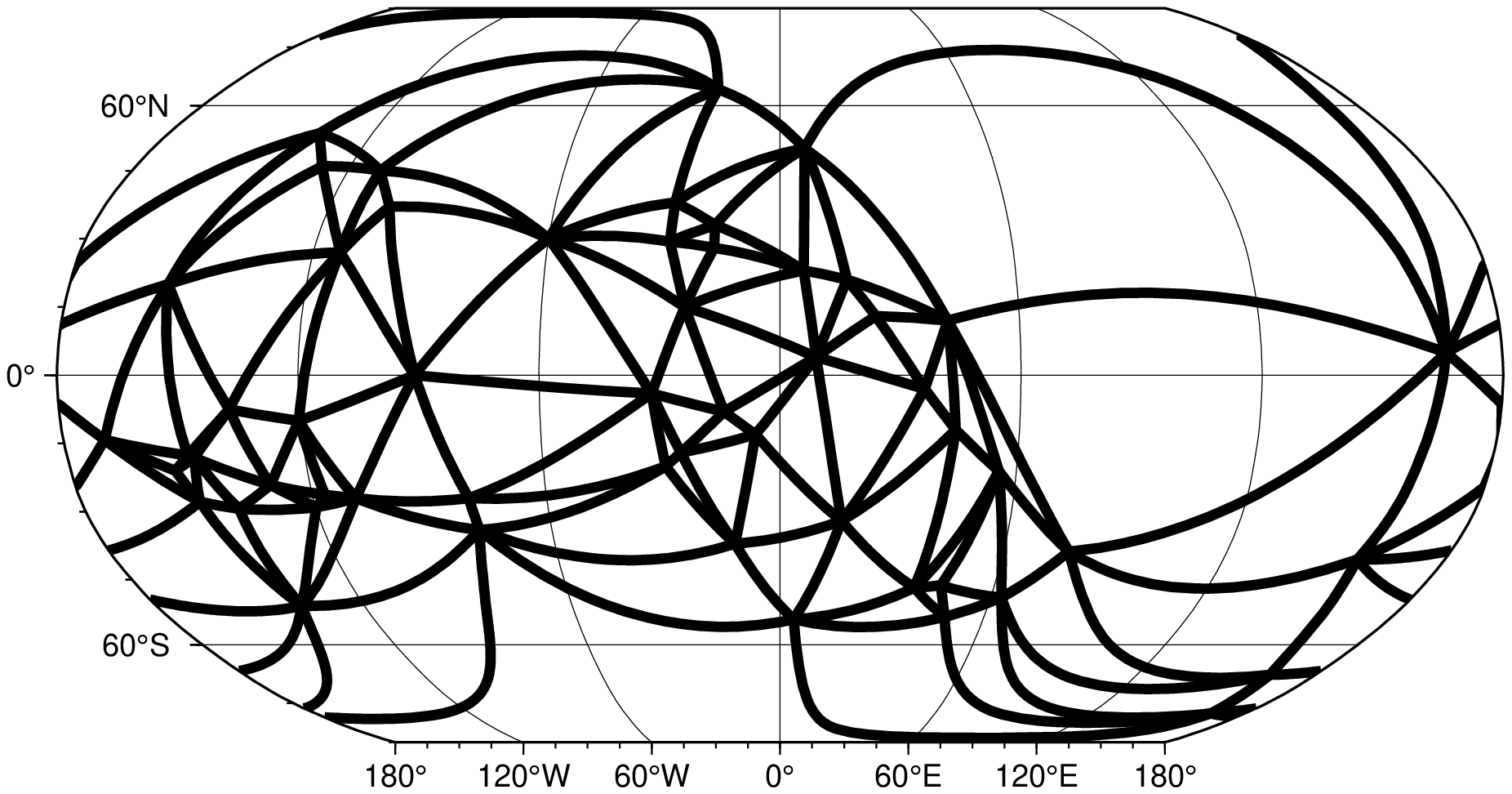
To create a spherical triangulation from the remote data set hotspots.txt and then plot it on a sphere, try:
using GMT
D = sphtriangulate("@hotspots.txt", voronoi=:d, arcs=true)
imshow(D, region=:global, proj=:guess, frame=:afg, pen=3)To triangulate the points in the file testdata.txt, and make a Voronoi diagram via plot, use
D = sphtriangulate("testdata.txt", voronoi=:v)
plot(D, region=:global, proj=(name=:ortho, center=(30,30)), pen=1, frame=:ag, show=true)To compute the optimal Delaunay triangulation network based on the multiple segment file globalnodes.txt and save the area of each triangle in the header record, try
D = sphtriangulate("globalnodes.txt", voronoi=:d, area=true)Notes
The STRIPACK algorithm and implementation expect that there are no duplicate points in the input. It is best that the user ensures that this is the case. GMT has tools, such as blockmean and others, to combine close points into single entries. Also, sphtriangulate has a skipdup option to determine and exclude duplicates, but it is a very brute-force yet exact comparison that is very slow for large data sets. Detection of duplicates in the STRIPACK library will exit the module.
See Also
References
Renka, R, J., 1997, Algorithm 772: STRIPACK: Delaunay Triangulation and Voronoi Diagram on the Surface of a Sphere, AMC Trans. Math. Software, 23\ (3), 416-434.
These docs were autogenerated using GMT: v1.11.0