Compute Euler Pole of rotation

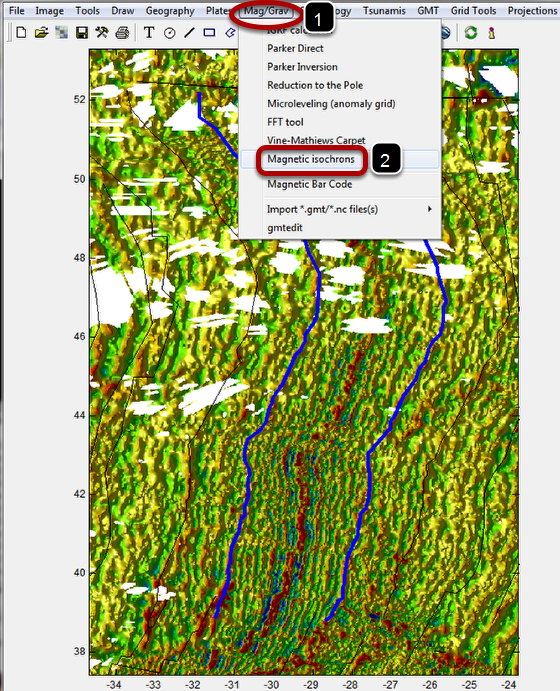
Follow the first steps of the "Fine picking of a magnetic isochron" lesson to create a display of the magnetic anomaly grid. Next, we will use the Mirone's internal dataset to plot magnetic isochrons. To do that do the steps shown at (1) and (2). To enhance the anomaly that we will use here the thickness and color of the anomaly 5 has been changes to blue and thick. Note that you can do something similar even when you do not have this grid. Since it will work only as a basemap any basemap will actually do.

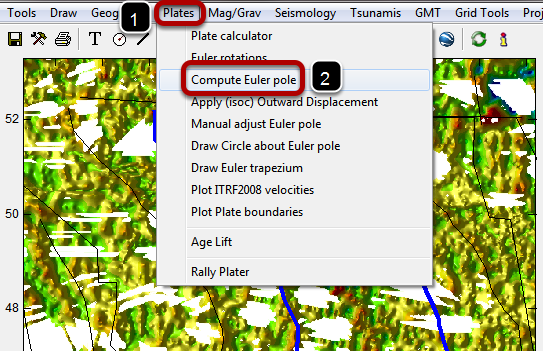
Just follow steps (1) and (2) to call the tool shown in next figure.

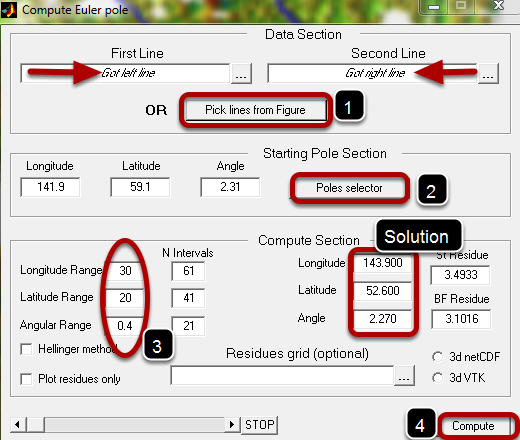
Hit the button "Pick lines from Figure" (1) to select the two lines that you want to fit by Euler rotation. Each line is selected by a double left-click. At the end of this step you should have the boxes pointed by the arrows filled like they show here. Second step (2) is to provide an initial guess. We do that by calling another tool that shows up when hit "Poles selector" (2). We don't show that tool here. Alternatively, fill the boxes manually. The step (3) selects the solution space that will be searched to find the best fit pole. Finally hit "Compute" (4) and see the movie of the systematic search.

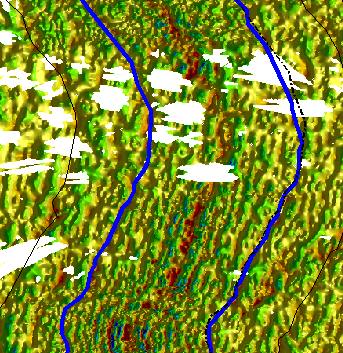
The black dashed line shows the result of rotation the West isochron 5 with the pole parameters computed in this exercise and that are displayed in previous figure under the "Solution" tag. At this point you could run the computation again using as starting point the previously computed solution, reduce the search domain and continue until the solution doesn't change anymore.