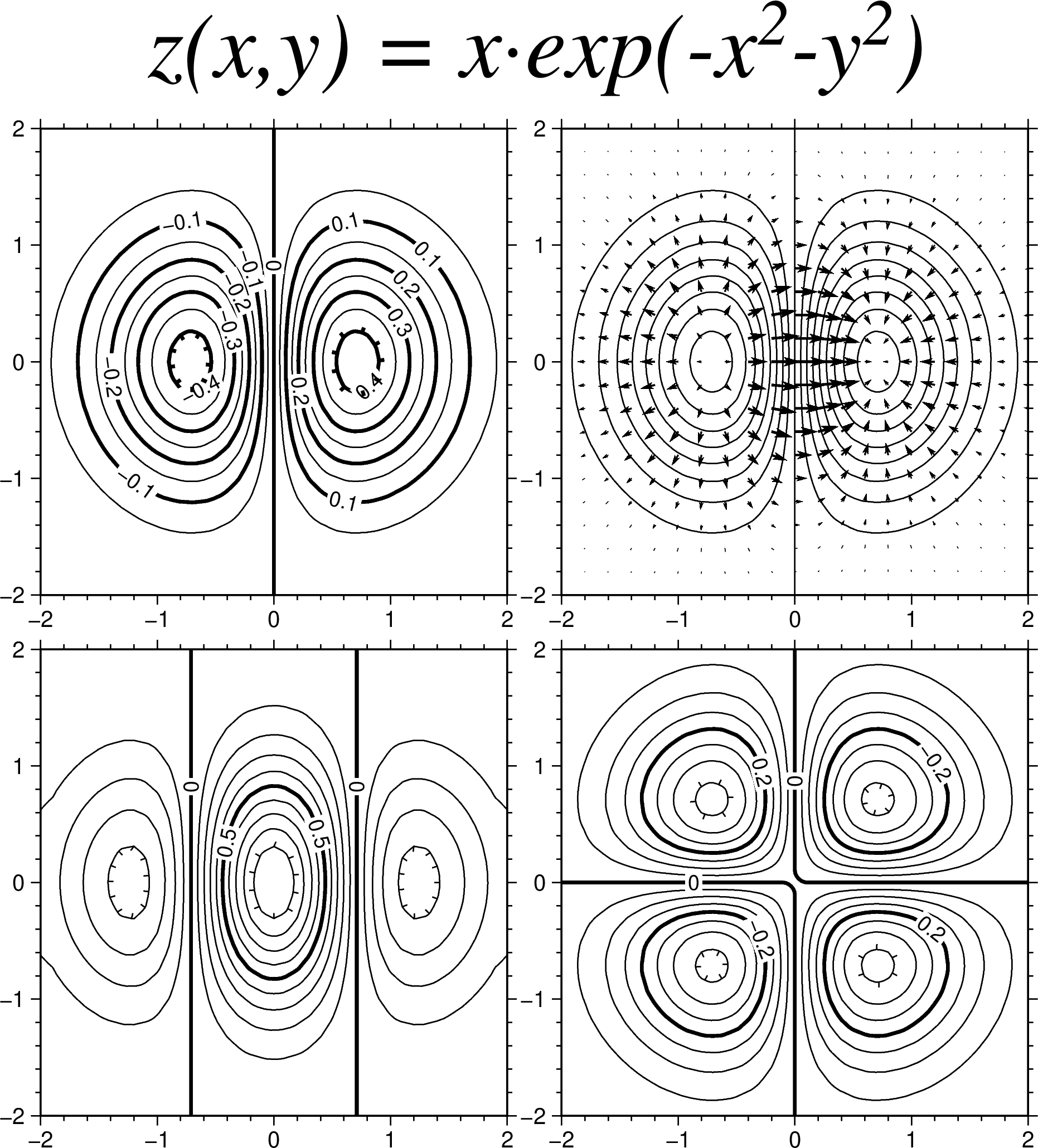
(13) Plotting of vector fields
In many areas, such as fluid dynamics and elasticity, it is desirable to plot vector fields of various kinds. GMT provides a way to illustrate 2-component vector fields using the grdvector utility. The two components of the field (Cartesian or polar components) are stored in separate grid files. In this example we use grdmath to generate a surface and to calculate by returning the x- and y-derivatives separately. We superpose the gradient vector field and the surface z and also plot the components of the gradient in separate windows. A text call to place a header finishes the plot
using GMT
gmtset(FONT_HEADING="40p,Times-Italic",)
Gz = gmt("grdmath -R-2/2/-2/2 -I0.1 X Y R2 NEG EXP X MUL =");
Gdzdx = gmt("grdmath ? DDX", Gz);
Gdzdy = gmt("grdmath ? DDY", Gz);
subplot(grid=(2,2), splot_size=15, margins=0.1, title="z(x,y) = x@~\327@~exp(-x@+2@+-y@+2@+)")
grdcontour(Gz, cont=0.05, annot=0.1, labels=(dist=5,), smooth=4, ticks=(gap=(0.25,0.08),))
subplot(:set, panel=(1,2))
grdcontour(Gz, cont=0.05, labels=(dist=5,), smooth=4)
grdvector(Gdzdx, Gdzdy, inc=0.2, arrow=(len=0.25, shape=0.5, stop=true, norm=0.6),
fill=:black, pen=1, vec_scale=2)
subplot(:set, panel=(2,1))
grdcontour(Gdzdx, cont=0.1, annot=0.5, labels=(dist=5,), smooth=4, ticks=(gap=(0.25,0.08),))
subplot(:set, panel=(2,2))
grdcontour(Gdzdy, cont=0.05, annot=0.2, labels=(dist=5,), smooth=4, ticks=(gap=(0.25,0.08),))
subplot("show")
© GMT.jl. Last modified: October 05, 2023. Website built with Franklin.jl and the Julia programming language.
These docs were autogenerated using GMT: v1.11.0