The longest sail

GMT uses the coast utility to access a version of the GSHHG data specially formatted for GMT. The GSHHG data have strengths and weaknesses. It is global and open source, but is based on relatively old datasets and hence may not be accurate enough for very large-scale mapping projects. For more information about the coastlines data-set see the GSHHG repository. We are referring this because the GMT coastlines were used to refine the solutions for the departing and arrival points of the longest sail.

Quoting Rohan Chabukswar and Kushal Mukherjee

There has been some interest recently in determining the longest distance one can sail for on the earth without hitting land, as well as in the converse problem of determining the longest distance one could drive for on the earth without encountering a major body of water.

Those authors have developed an algorithm for calculating the longest straight-line path on land or sea and came out with a solution for the maritime path that starts in Pakistan (66:40 E; 25:17 N) and ends in the Kamchatka Peninsula (162:14 E; 58:37 N) following a great circle of 32,090 kilometers long. However, as they acknowledge, the computation was performed using a topo-bathymetric grid with a grid step of 1 arc minute (~1.8 km) and on a spherical Earth.

The first effect, that of the grid spacing, adds only a very small error in the total length because the start and end points actually fall on land. Moving them to the intersection of the great circle with the GMT coastlines data-set ((66:39:49 E; 25:16:45 N), (162:20:44 E; 58:35:50 N)) leads to slightly shorter path of 32,083.3 km. Here we used authalic sphere computed from the WGS84 ellipsoid. The second effect, that of the spherical vs ellipsoidal approximation, is what we will see here. We will show that the proposed locations still works for an ellipsoidal Earth but that we can find a slightly longer geodesic line in the vicinity of the spherical solution, though not mathematically prove it is the longest possible geodesic.

Sherical (great circle path)

To start with, let us look how close to land the great circle solution has come. On its closest approach in the Aleutian archipelago a check with GoogleEarth imagery shown that it came as close as ~250 meters from land. Another location where it also came very close was in the Comoros archipelago (~750 m).

The following script produces the map below. To obtain the other solutions, also shown below, change the Booleans in the first three lines.

best = false		# First precedence (if true computes the ellipsoidal solution)   
sphere = true		# Second precedence (if true computes the spherical solution)
PakKam = false		# If all 3 are false ==> KamPak	(compute geodesics with original points moved to shore)

# Set titles, fig names and regions for the insets depending on the selected solution.
if (best)
	ptPak = [66.6424435 25.2972055];		ptKam = [162.34545111 58.59724279];		# New ~Best [66:38:32.8 25:17:49.9]
	x = geodesic(ptKam, ptPak, longest=true, step=10000);
	title, fname = "~Best Ellipsoidal", "Longest_best_ellipse.png"
	subtit = "Length = $(round(parse(Float64, x.attrib["Length"]) / 1000, digits=3)) km"
else
	ptPak = [66.66366872 25.27917480];		ptKam = [162.34545111 58.59724279];		# Intersect Orig with shoreline
	if (sphere)
		x = geodesic(ptPak, ptKam, longest=true, step=10000, proj="+proj=lonlat +a=6371007 +b=6371007");
		title, fname = "Spherical", "Longest_sphere"
		subtit = "Length = $(round(parse(Float64, x.attrib["Length"]) / 1000, digits=3)) km"
	else
		x = geodesic(ptPak, ptKam, longest=true, step=10000);
		title, fname = "Ellipsoidal Pak->Kam", "Longest_ellipse_PakKam.png"
		subtit = "Length = $(round(parse(Float64, x.attrib["Length"]) / 1000, digits=3)) km"
	end
end

# Make the plot
gmtbegin(fname)
	coast(region=:global, proj=:guess, shore=0.5, land=:gray, frame=:auto, area=(500,1), title=title, subtitle=subtit)
	plot(x, lw=0.5, lc=:red)

	# Comoros
	plot([42.0 -14.0 46.0 -10.0], marker="r+s", ml=(0.2, :blue))    # A blue rectangle
	inset(inset_box=(map=true, anchor=(56,0), justify=:TL, width=1.4), box=(fill=:white, pen=(0.5, :blue)))
		coast(region=[43.1, 44.6, -12.7, -11.2], frame=:none, shore=0.5, land=:orange, figsize=1.4)
		plot(x, lw=0.5, lc=:red)
		if (best || sphere)
			plot([43.8 -12.45 44.00 -12.25], marker="r+s", ml=(0.2, :darkblue))    # A blue rectangle for 2nd zoom
		end
	inset(:end)
	inset(inset_box=(map=true, anchor=(62,-40), justify=:TL, width=(1.5,1.0)), box=(fill=:white, pen=(0.5, :darkblue)))
		coast(region=[43.850, 43.93, -12.41, -12.32], frame=:none, shore=0.5, land=:darkorange, figsize=1.5)
		plot(x, lw=0.5, lc=:red)
		just = (PakKam) ? :BL : :BR
		basemap(map_scale=(anchor=just, scale_at_lat=-12.35, length="4k", label=true, fancy=true, offset=(0.1,0.3)),)
	inset(:end)

	# Kamchatka
	inset(inset_box=(map=true, anchor=(140,48), justify=:TL, width=1.5), box=(fill=:white, pen=(0.5, :blue)))
		coast(region=[161.7, 164.0, 57.67, 59.5], frame=:none, shore=0.5, land=:orange, figsize=1.5)
		plot(x, lw=0.5, lc=:red)
		plot(ptKam, marker=:circ, ms=0.1, fill=:darkred)	# Orig pt
	inset(:end)

	# Aleutian
	plot([-178.2 50.49 -173.3 52.77], marker="r+s", ml=(0.2, :blue))    # A blue rectangle
	inset(inset_box=(map=true, anchor=(-158,40), justify=:TR, width=(1.5,1)), box=(fill=:white, pen=(0.5, :blue)))
		R = (best || sphere || PakKam) ? [-175.7, -175.3, 51.90, 52.1] : [-175.325, -175.08, 51.97, 52.067]
		coast(region=R, frame=:none, shore=0.5, res=:full, land=:orange, figsize=1.5)
		plot(x, lw=0.5, lc=:red)
	inset(:end)
	if (false && best || sphere)
		inset(inset_box=(map=true, anchor=(-175,5), justify=:TL, width=(1.6,1.4)), box=(fill=:white, pen=(0.5, :darkblue)))
			R = (best) ? [-175.6, -175.48, 51.945, 52.05] : [-175.60, -175.538, 51.950, 52.07] 
			coast(region=R, frame=:none, shore=0.5, res=:full, land=:darkorange, figsize=1.6)
			plot(x, lw=0.5, lc=:red)
			if (best)
				basemap(map_scale=(anchor=:BC, scale_at_lat=52, length="2k", label=true, fancy=true, offset=(-0.1,0.3)),)
			else
				basemap(map_scale=(anchor=:BR, scale_at_lat=52, length="2k", label=true, fancy=true, offset=(0.1,0.3)),)
			end
		inset(:end)
	end

	# Pakistan
	inset(inset_box=(map=true, anchor=(63,30), justify=:BL, width=1.4), box=(fill=:white, pen=(0.5, :blue)))
		coast(region=[66.0, 66.8, 25.1, 25.9], frame=:none, shore=0.5, res=:full, land=:orange, figsize=1.4)
		plot(x, lw=0.5, lc=:red)
		plot(ptPak, marker=:circ, ms=0.1, fill=:darkred)	# Orig pt
	inset(:end)
gmtend(:show)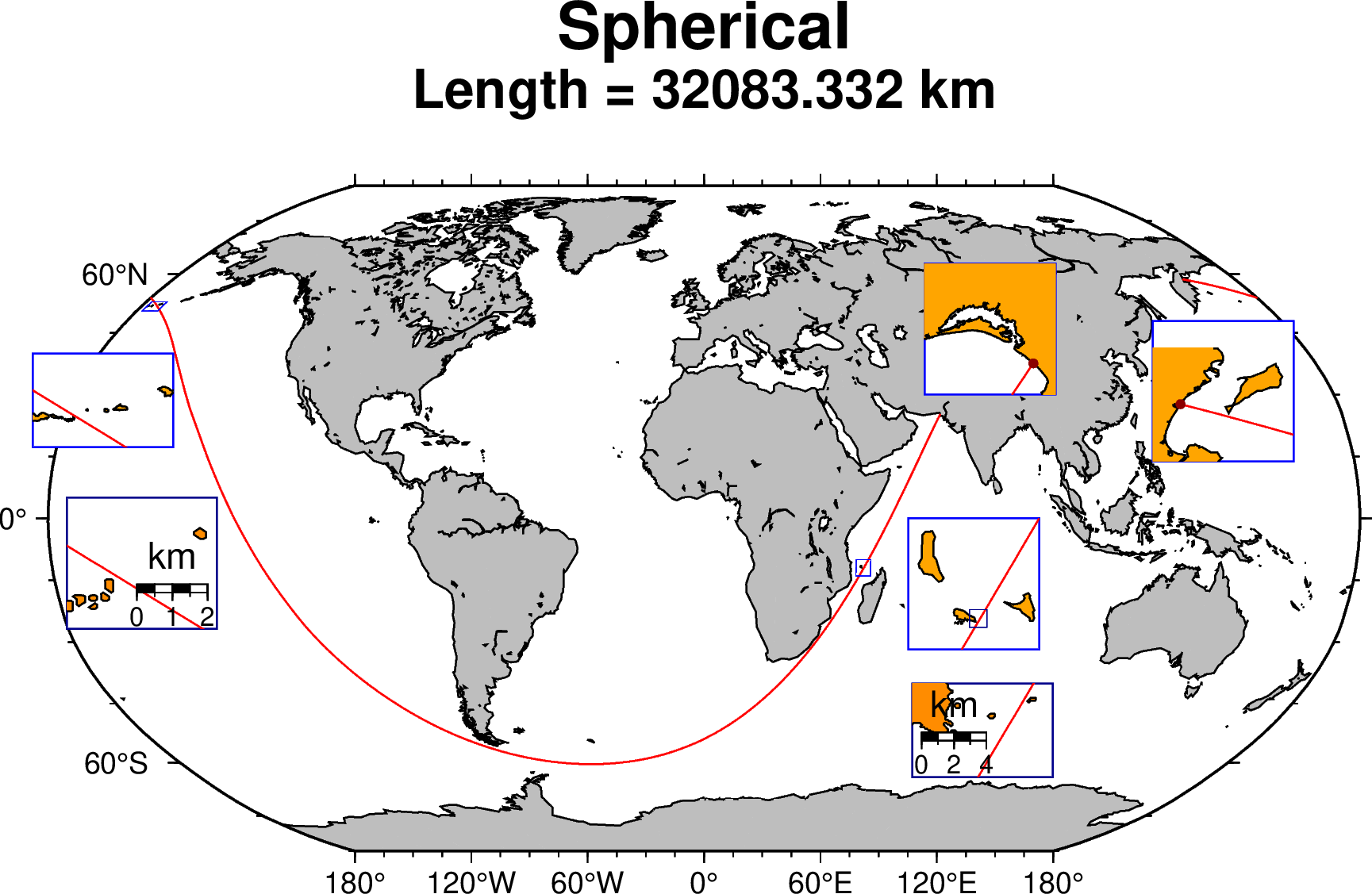

Ellipsoidal (geodesics)

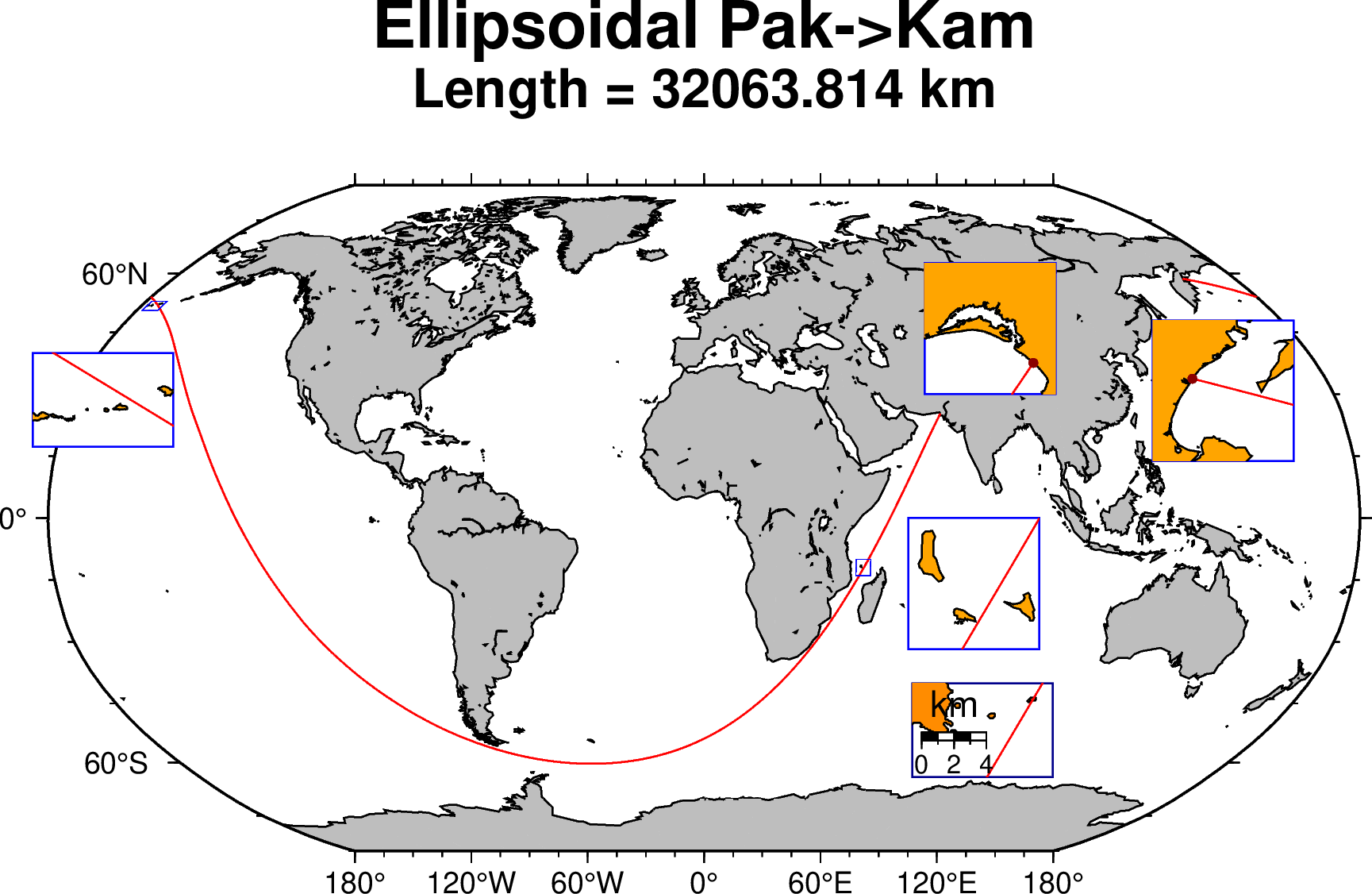
Now let's see how it behaves if we compute the path along the shortest distance on an ellipsoid (a geodesic line), the WGS84 ellipsoid in this case. Good, but the case not so simple as a geodesic, except for along a meridian or the equator, is not a closed line. That means, following a geodesic that starts at a certain azimuth different from +/-90 or 0 degrees we don't return to starting point, see this Wiki page. So this means we cannot simply compute the other way around as the complement of the shortest path between A and B as that is a too crude aproximation. For more details on this problem see this discussion in the GMT forum that shows also the history on how this problem was solved. But the take of this is that one can obtain a geodesic line that very closely (at the decimeter level) can go from A to B and be a reversible solution. That is, if we swapp A and B we get the same solution.

Next figure shows that the proposed geocentric solution still holds for the ellipsoidal case. Well, the figure doesn't show that because we can see an interruption due to a hit in one of the Comoro's islet. However, this is not really true because the GMT shorelines at this levels show the effect of having been digitized from last century charts and are off often off by ~250-300 m. And in fact, checking with GoogleEarth we would see that the path manages to go through those rocks without hitting them.

A slightly longer geodesic solution

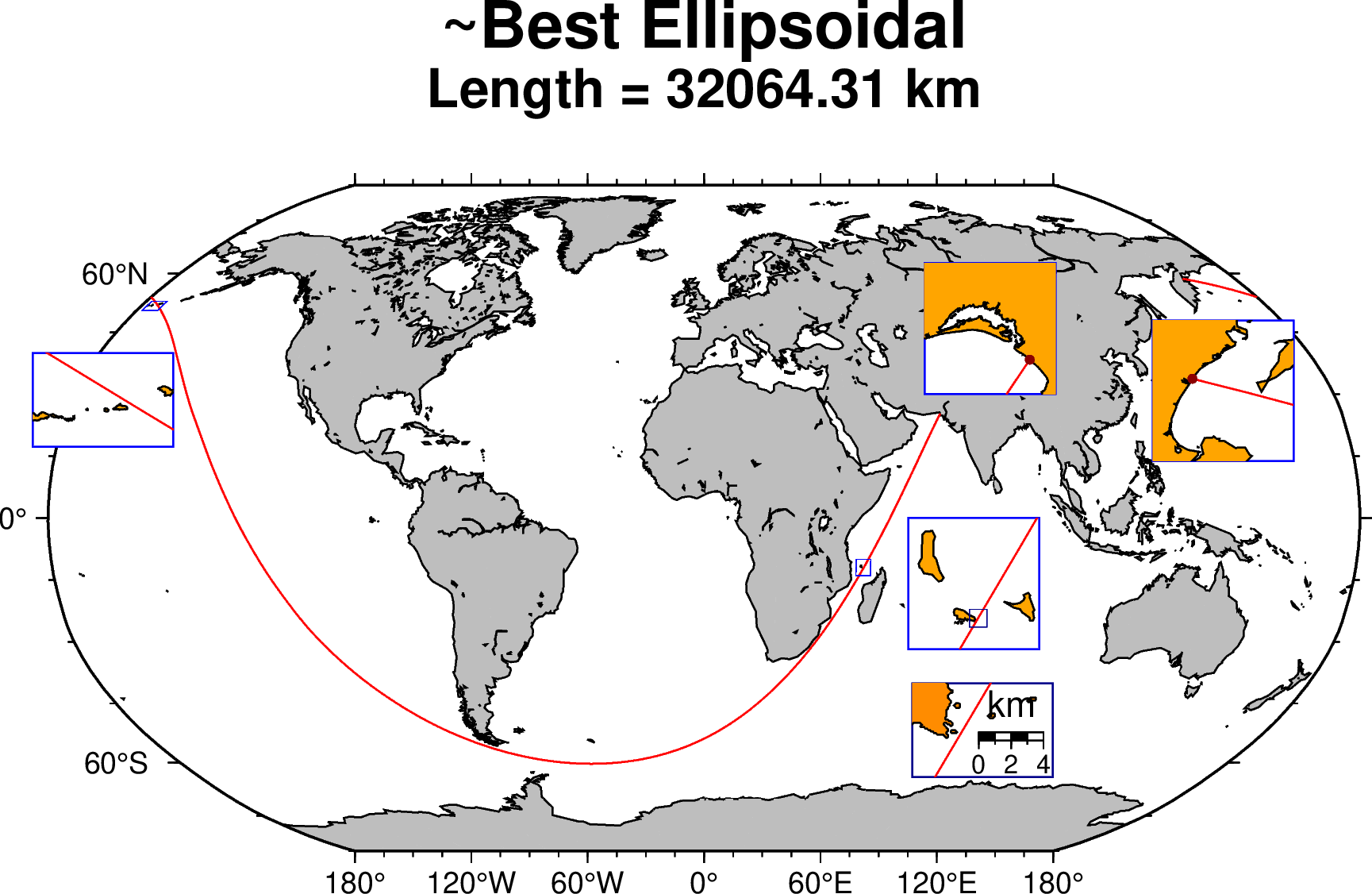
Although the solution proposed by Chabukswar and Mukherjee still holds on the ellipsoidal Earth, it is possible to find a nearby alternative that is slightly longer. With trial an error it was possible to find one that adds ~0.5 km to the that path. That solution, that starts at [66:38:32.8 E; 25:17:49.9 N] and ends at the same Kamachatka point of [162:20:44 E; 58:35:50 N] is shown in the figure below and has a length of ~32,064.31 km.